Modern radar systems serve a broad range of commercial, civil, scientific and military applications. In addition to the traditional application areas of military, weather and law enforcement, radar technology is utilized in automotive and public transportation safety features, global mapping, oil exploration and even quality control for manufacturing methods requiring surface precision or material integrity. A variety of radar techniques have emerged to support this broad range of application areas. However, the fundamental ability of a radar system to process reflected radio frequency (RF) information and to identify the parameters of location, speed and direction of an object remains the primary and most utilized function of modern radar.
Most radar systems use a pulsed microwave signal directed toward the object of interest, to collect the reflected energy via the same transmitting antenna. However, some systems achieve this measurement by using Frequency-Stepped Chirped Radar (FSCR) signals to transmit pulsed, linear frequency ramps (also known as chirps). The FSCR radar is distinguished by its ability to achieve a high range resolution in a system that has limited instantaneous bandwidth. Successive pulses increase linearly in discrete steps. The pulse modulated signal is transmitted using an antenna. The echo signal reflected back is combined with the transmitted signal to create a beat signal to calculate the round trip time, which is inversely proportional to the bandwidth (BW). Range resolution is the ability to distinguish between two different targets at the same bearing with two different ranges [Pourvoyeur, et al.]. With c being the speed of light, the Range Resolution is given as
Range Resolution=c*1/2BWh
fn=fo+ n∆f
The transmitter frequency is linearly stepped from fo, the starting carrier frequency while ∆f represents the frequency step size.
n=1…N; each burst equals N pulses
Because the bandwidth is proportional to N∆f by rewriting the range resolution equation with stepped frequency yields
Range Resolution=c*1/2N∆f
A linear stepped frequency system achieves wide bandwidth by achieving N∆f with multiple pulses. This is a powerful method since the range resolution can be improved by changing N∆f. FSCR technique allows radar systems to achieve better range resolution with a design that implements a low instantaneous bandwidth and a relatively low sampling rate ultimately lowering cost and reducing system complexity. The right design tools lead to a highly predictive design that facilitates hardware verification prior to the significant non-recurring expenses and re-spin of custom microwave components.
Key functions of the radar system can be modeled in software with commercial off-the-shelf hardware. In most radar systems, the transmitter shares a common oscillator with the receiver. By using a high frequency coupler, the same oscillator is a stimulus for the mixer on the receiver. A duplexer allows the radar system to transmit and receive in different time periods.
The radar receiver includes mixers, amplifiers, switches, isolators, phase detectors, analog to digital circuitry and signal processors. Accurate timing, phase and frequency measurements between transmit and receive signals enable the radar system to determine target range and velocity. Because the target is mobile, the received signal will exhibit a Doppler shift.
Differentiating between Doppler shift caused by clutter (objects not of interest) and the true object is a mathematically intensive problem. A moving target detection (MTD) caused by clutter can generate a false alarm. One way to mitigate this effect is to add additional sensors. The target position is obtained by triangulating the bearing measurements from each pair of sensors [Alexiev, et al 1998]. Figure 1 shows a system with two sensors where the triangulation measurement yields four results (A, B, C & D) for the two actual targets which would result in a false alarm. The number of false detections will increase as more targets are added. Also, a chirped radar system can create its own Doppler-coupling effects.
Figure 1: Sensors with Two Different Approaching Targets
A good radar system model will assist the evaluation of a communication system. Built into the AWR’s Visual System Simulator (VSS) radar system library are a number of tools, such as Constant False Alarm Rate (CFAR) detector, MTD and Probability of Detection (POD) indicators. This type of signal processing is typically implemented using Digital Signal Processing (DSP) in the receiver baseband (post RF-signal detection).
To build a representative model, the chirp signal as well as the quality of the receiver must be characterized to simulate real world scenarios of multiple targets. By collecting the echoes from the chirped pulses and applying matched filtering and stochastic techniques, the image can be re-constructed with dimensional accuracy.
A host of computer generated algorithms exist for radar signal processing to identify clutter and to reduce false alarms. Nevertheless, the implementation of more complex algorithms can be time consuming, especially when broadband coherent or correlated demodulation is required. FSCR systems can be modeled easily using a broadband DSP capable receiver. In order to capture the frequency and time domain information for radar signals, one requires a wideband vector signal analyzer such as the NI-5668R 26.5 GHz VSA. This instrument features up to 765 MHz of instantaneous bandwidth and contains a programmable FPGA which can be used to simulate detection algorithms.
Today’s hardware and software tools provide the ability to dramatically improve the design efficiency, cost effectiveness and performance of advanced radar architecture by providing capabilities to:
[a] Derive the system constraints through a systematic budget analysis which accounts for backend-processing, dynamic range, noise figure and scan rate.
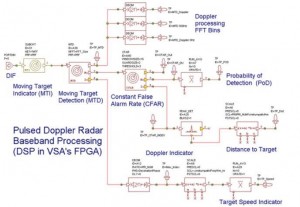
[b] Build a model similar to the Pulse Doppler Radar System shown in the references section [AWR, 3] using empirical results and data files for sub-components.
[c] Model sub-components in the system by using empirical results– an example is provided below for an important part of a Radar Cross-Section (RCS) model.
[d] Analyze the system level modeling data and optimize the design to meet specifications.
[e] Prototype the design by using commercially available products.
[f] Extend the hardware system by adding receivers to simulate multiple sensors.
AWR’s VSS is capable of performing a wide range of radar system model complexity. An example model of a Pulsed Doppler system with chirp is shown in Figure 2.
Figure 2 – VSS Model for the radar transmitter and receiver front-end.
Utilizing VSS, the components of a basic radar architecture can be modeled using system level primitives, including actual or predicted s-parameter data files. For example, a Chirp Generator is specified using performance characteristics while the antenna is modeled using an actual RCS pattern.
After the chirped signal is transmitted and reaches the target, the reflected signal is detected by the antenna and passed to the receiver. Figure 3 shows the receiver block diagram. The NI-5668R VSA has a Kintex-7 FPGA that can be programmed to model the receiver’s various matched filter responses to differentiate the signal of interest from clutter by applying advanced detection schemes.
Figure 3 reveals the NI-5668R VSA components: downconverter, software, firmware and hardware combined to model a basic radar architecture. The final intermediate frequency is digitized directly in order to avoid quadrature and offset errors that are common to zero-IF systems, thus avoiding calibration of the IQ impairments. At the heart of the NI-5668R baseband processor is the DSP engine, a Kintex-7 FPGA. The FPGA serves two purposes: 1) communicates directly with the host program, processes and controls the flow of data over the bus to the host computer 2) performs the complex DSP algorithms on the digitized baseband signal. The VSA’s large instantaneous bandwidth of 765 MHz allows the true microwave signal to be captured up to 26.5 GHz. Spectral distortion is avoided by capturing the entire wideband pulse in a single data acquisition.
Figure 3 – Hardware / Firmware / Software Architecture of the NI-5668 VSA
Signal Processing in Radar Systems
A representative signal processing chain for detection is shown in Figure 4. The computational algorithm for identifying targets and Doppler processing can be implemented in the FPGA.
Figure 4 – VSS simulation of the baseband DSP implemented within the NI-5668R
The notional model of the DSP section, depicted in Figure 4, consists of an array of demodulators and threshold detectors. Fast Fourier Transform (FFT) can be used to differentiate the Doppler components; however, the frequency spacing(s) could also be dynamic and uneven, as in the case with FSCR. Implementation of FSCR requires precise synchronization with the frequency step, along with coherent demodulation. In modern DSP based receivers, increased bandwidth and coherent Digital Down Converters (DDCs) can be used to the design a broadband FSCR system while maintaining dynamic range.
Generating a Frequency-Swept Chirp Example
A stepped chirp can be derived from a continuous chirp, but the pulses gate the frequency ramp as shown in Figure 5. In practice, the pulses can be modified with a window function, rather than using simple rectangular pulses. A Kaiser window is used in this example, and the data will show a more efficient spectral footprint.
Figure 5 – Illustration of the frequency ramp & windowed pulse timing to generate the FSCR IQ waveform
With complex waveforms, it is easier to realize the system using an Arbitrary Waveform Generator (AWG). The pulses gate the IQ sweep generation of the AWG. Note the pulse shaping in time domain due to the Kaiser window function. For the programming example in figure 6, LabVIEW Mathscript is chosen because its syntax is familiar to DSP programmers. The input parameters “wn” and “Ns” correspond to the window smoothing factor and the number of frequency steps.
Figure 6 – Mathscript code to verify the FSCR theoretical model and program the AWG
Next, let’s compare the modeled spectrum of the FSCR signal to the measured spectrum. They both show nearly 15 dB suppression between frequency bins, an ultimate out-of-band rejection of at least 40 dB relative to any frequency peak and more than 66 dB relative to the total channel power of -26 dBm. In theory, each of the five spectral components will also share power equally, since the maximum spectral energy for each pulse is centered on its frequency at the time of the chirp. Parseval’s Theorem states:
Where
energy per pulse ,
NP = number of pulses, and NB = number of frequency bins. NP=NB.
So the integrated power in the frequency bins should equal the sum of the power of all the pulses. By extension, assuming each pulse has a unique frequency, each pulse’s energy in the frequency domain will be equally weighted and will be equal to 1/Ns of the total energy. Let’s check the measurement in Figure 7:
Figure 7 – Comparison of the spectral power in one frequency bin vs. the total
The measured power in the central 20 MHz portion of the FSCR spectrum is -32.71 dBm and the entire spectrum measures -25.9 dBm.
The measured power ratio is:
Figure 8 compares the measured spectral efficiency due to the Kaiser windowing of the pulse envelope. The windowed version shows nearly a 20 dB improvement in the adjacent channel.
Figure 8 – Measured result of Kaiser windowed (left) vs. rectangular pulses (right)
Modern radar systems are more complex due to signal processing algorithms designed to eliminate false detections, to identify multiple targets and to span multiple sensors. At the same time, the system should be designed for maximum spectral efficiency and dynamic range. FSCR systems are signal processing intensive, so it is imperative to model the hardware and numerical algorithms to achieve these goals. The front end receiver of radar systems can be replaced with instrumentation which enables validation of target detection schemes. Using VSS, the PXI Platform and wideband VSAs in conjunction, an advanced radar system can be created.
Reference:
1) K. Pourvoyeur, R. Feger, S. Schuster, A. Stelzer, L. Maurer, Ramp Sequence Analysis to Resolve Multi-target Scenarios for a 77-GHz FMCW Radar Sensor
2) Alexiev, K and Bojilov, L, A Hough Transform Track Initiation Algorithm for Multiple Passive Sensors, Bulgarian Science Fund, Grant No. I-801/98
3) https://awrcorp.com/download/faq/english/examples/Pulse_Doppler_Radar_System.aspx
